Numerical Methods - Euler Method Part 3
Numerical Methods for Solving Differential Equations
Euler's Method
Theoretical Introduction
(continued from last page...)
Deriving the Euler's Method Formulas
Reminder: We're solving the initial value problem:
y′ = f(x, y)
y(xo) = yo
As we just saw in the graphical description of the method, the basic idea is to use a known point as a "starter," and then use the tangent line through this known point to jump to a new point. Rather than focus on a particular point in the sequence of points we're going to generate, let's be generic. Let's use the names:
- (xn, yn) for the known point
- (xn+1, yn+1) for the new point
Our picture, based on previous experience, should look something like this:
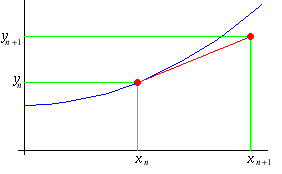
(Though the proximity of the true solution to the point (xn, yn) is, perhaps, a little optimistic.)
Our task here is to find formulas for the coordinates of the new point, the one on the right. Clearly it lies on the tangent line, and this tangent line has a known slope, namely f(xn, yn). Let's mark on our picture names for the sizes of the x-jump, and the y-jump as we move from the known point, (xn, yn), to the new point. Let's also write in the slope of the tangent line that we just mentioned. Doing so, we get:
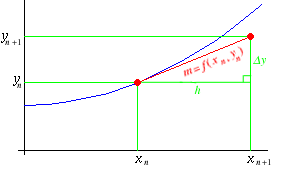
The formula relating xn and xn+1 is obvious:
xn+1 = xn + h
Also, we know from basic algebra that slope = rise / run, so applying this idea to the triangle in our picture, the formula becomes:
f(xn, yn) = Δy / h
which can be rearranged to solve for Δy giving us:
Δy = h f(xn, yn)
But, we're really after a formula for yn+1. Looking at the picture, it's obvious that:
yn+1 = yn + Δy
And, replacing Δy by our new formula, this becomes:
yn+1 = yn + h f(xn, yn)
And that's it! We've derived the formulas required to generate a numerical solution to an initial value problem using Euler's Method. Let's go and look at a summary of the method.







