Solving the Preliminary Example

continued from last page...)

Your latest session should look like this:

y[t]-x[t]-E^(3t)/.{x[t]->E^(-t),y[t]->E^(3t)}

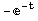
which tells us the value of the right hand side of equation (1). Comparing this with what we got on the previous command for the left hand side, we see that they are the same. So far, so good. Substituting the proposed solution into both sides of the equation yields the same result, i.e. renders the equation a true statement. All we need to do now is check to see whether our solution works on the second equation.

We check the second equation in the same way that we checked the first, by making substitutions into both sides individually, and checking to see if the results are equal. The commands required are very similar to the ones we just made, so I'm leaving it up to you to check the other equation. (It will take two commands, remember.)

Well don't just sit there, go back to Mathematica and get on with it! Come back here when you're done.

We'll now see what you should have gotten...

If you're lost, impatient, want an overview of this laboratory assignment, or maybe even all three, you can click on the compass button on the left to go to the table of contents for this laboratory assignment.