Solving the Preliminary Example
continued from last page...)
Your little session should look like this:
D[x[t]/.x[t]->E^(-t),t]
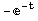
Now remember, this is the value of the left hand side of the first equation. To complete our verification of the proposed solution we have a lot more work to do. (Three more commands, in fact, since there are four "sides" in all.)
Since we're on a new page, let me remind you again of the problem and proposed solution.
| Problem | Proposed Solution | |
|---|---|---|
| (1) | x' = y - x - e3t | x(t) = e- t |
| (2) | y' = 3y + 2x - 2e- t | y(t) = e3t |
As we said a moment ago, so far we have verified the value of the left hand side of the first equation. We must now check it's right hand side.
The command we need to substitute both the x(t) and y(t) value into the right hand side of equation (1) is:
y[t]-x[t]-E^(3t)/.{x[t]->E^(-t),y[t]->E^(3t)}
Jump back to Mathematica and try it. (Remember, you can "cheat" on the typing by using Copy and Paste.)
We'll now see what you should have gotten...
 |
If you're lost, impatient, want an overview of this laboratory assignment, or maybe even all three, you can click on the compass button on the left to go to the table of contents for this laboratory assignment. |