Solving the Preliminary Example

continued from last page...)

Your check of equation (2) should look like this:

D[y[t]/.y[t]->E^(3t),t]



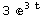
3 y[t]+2 x[t]-2 E^(-t)/.{x[t]->E^(-t),y[t]->E^(3t)}


 

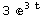
Clearly both sides give the same result, making the second equation true when you substitute the proposed solution into it. We have now verified that the proposed solution does indeed satisfy both differential equations in the system. We say that we have found a solution of the system. We can't claim that we've found the system's general solution, since that would be a family of solutions. What we've found is just a single member of that family.

Let's go and tackle the problem more seriously, putting Mathematica's "big guns" to work.

If you're lost, impatient, want an overview of this laboratory assignment, or maybe even all three, you can click on the compass button on the left to go to the table of contents for this laboratory assignment.