Slope Fields with Mathematica - Exercise 3

Equations of the Form: dy/dx = g(x, y)

Exercises

For each exercise, make a note of the problem, (both the differential equation and plot bounds), then switch to Mathematica and create the slope field by clicking on the "try it" link. Remember, once again you'll be entering your own parameters. When you return you may verify your answer and read any applicable comments about the problem by clicking on the "discuss it" link. (Only choose this option once you've done the problem yourself in Mathematica.)

  1. dy/dx = x y, on the region -3 ≤ x ≤ 3, and -3 ≤ y ≤ 3, no arrow-heads, including axes, default vector grid
  2. dy/dx = x + y, on the region -3 ≤ x ≤ 6, and -6 ≤ y ≤ 3, no arrow-heads, including axes, default vector grid
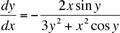  3. Equation, on the region -3 ≤ x ≤ 3, and -3 ≤ y ≤ 3, no arrow-heads, including axes, 25 X 25 vector grid
  4. dy/dx = y2 + y/x, on the region -1 ≤ x ≤ 1, and -1 ≤ y ≤ 1, no arrow-heads, including axes, default vector grid

Well, hopefully you had some success doing those exercises by yourself. Now that we've had some practice with this even more general class of differential equation it's time to make some general observations.

 

Compass If you're lost, impatient, want an overview of this laboratory assignment, or maybe even all three, you can click on the compass button on the left to go to the table of contents for this laboratory assignment.