Solving Differential Equations with Mathematica's Solver
(continued from last page...)
Did you get that right hand side figured out? The Mathematica mini-session you just had should have looked something like this:
Integrate[2x E^(x^2),x]
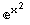
Integrate[Sin[y]^2 Cos[y],y]

Mathematica leaves off the constants of integration, so we must supply these mentally. It is worth noting here that Mathematica's integration of the right-hand side of the differential equation takes on a far different form from the result you would most likely get if you were to evaluate the integral by hand, (most likely by using substitution.) This kind of behavior is quite typical of most computer algebra systems, and can be fairly frustrating at times. Anyway, looking over your results, and setting both sides equal to one another, you should realize that the (implicit) solution to the original differential equation is:
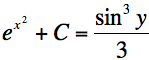
Notice that we have supplied the C ourselves. This solution could be made explicit with a little work, (multiply both sides by 3, take the cube root of both sides, and then the arcsine,) but that's not our main concern right now. We're here to learn about Mathematica's differential equation solver.
So what about this DSolve command?
Before we can use the DSolve command the differential equation must be put in derivative form, whereas in the original differential equation it's in differential form. To achieve the change we divide the original differential equation:
on both sides by dx, giving:
and replace the (dy/dx) by the notation y′ (y-prime):
We're about to feed this equation into Mathematica's DSolve command, but first a few notes and reminders of what we learned in the introductory labs:
Mathematica has three different versions of the equals sign that we usually don't bother to distinguish between when writing them on paper:
"=", the single equals sign. This is used when you want to move a value into a variable so that the variable has that value throughout the rest of your session. e.g. u=7 means that the next time u is used in the session, 7 is used in its place.
":=", the colon equals. This can be thought of as "delayed assignment". e.g. v:=w means that no value is immediately moved into v, but instead a "pointer" to w is established. The next time v is used in the session, the current value of w at that time is used in its place.
"==", the double equals sign. This is used as a logical operator comparing both sides of the equality to decide on whether the statement is true or false. e.g. a+b==5 would return True if a were 2 and b were 3, and False if a were 8 and b were 6. This form of equals sign is used when forming equations, including differential equations.
The sine function takes the form Sin[...], and the cosine function takes the form Cos[...], where you fill in the dots with the appropriate argument.
The number e is referred to as E in Mathematica.
It's been a while now since we asked for the syntax of the DSolve command, so I'll just remind you. ?DSolve returned the information "DSolve[eqn, y[x], x]" (among other things.)
Armed with all of the above information we should feel comfortable solving:
by entering the following command:
(Note the double equals sign, which is used since we're entering an equation as the first argument of the command.)
Go ahead and do so now by switching to Mathematica, typing it out and hitting [ENTER]. Don't be shocked by the error message, and come back here to your browser when you're done.
We now move on to discuss the message you were just assaulted with...







