Solving the Preliminary Example

continued from last page...)

The command should have returned the following result:

prelimsol= NDSolve[{x'[t]== y[t]- x[t]- E^(3t), y'[t]==3 y[t]+2 x[t]-2 E^(-t), x[0]==1,y[0]==1}, {x[t],y[t]},{t,-2,2}]

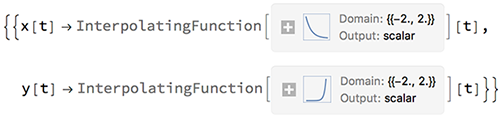
We've seen this form of solution before, and you may even have been expecting it. One difference, of course, from your previous labs is that the solution actually consists of two parts, the numerical solution for x(t), and the numerical solution for y(t). This makes sense if you think about it.

In the past we have repeatedly used something that I've referred to as the "[[1,1,2]] trick." Now that the solution has two parts, we need to be a little more careful. Remember, [[1,1,2]] refers to the result's first row, first column, second part. Looking carefully at our answer, you should be able to see that this refers to the x[t] value. So how would we grab the y[t] value? Well, y[t] is in the first row, second column of the solution, so to extract it's value we'd need to use a [[1,2,2]] trick. Be careful not to confuse these two! (If you're having trouble seeing the rows and columns, probably because of the way the matrix wraps around at the edge of the window, feel free to return to Mathematica and redisplay the result using the MatrixForm command.)

So let's get down to the job of grabbing the parts of the solution that we wish to use. We're going to pull the expressions for x[t] and y[t] into two separate variables, say prelimx and prelimy respectively. We can do so with the following pair of commands:

prelimx=prelimsol[[1,1,2]]
prelimy=prelimsol[[1,2,2]]

Go to Mathematica, and issue them both, but make sure to do them in separate cells! Come back to your browser when you're done.

Now let's look at what you should have gotten...

If you're lost, impatient, want an overview of this laboratory assignment, or maybe even all three, you can click on the compass button on the left to go to the table of contents for this laboratory assignment.