Euler Method - Using the Method with Mathematica - Part 5

Numerical Methods for Solving Differential Equations

Euler's Method

Using the Method with Mathematica

(continued from last page...)

Your commands should have resulted in:

prelimsol2=euler[x+2y, {x,0,1}, {y,0}, 20]

{{0, 0}, {0.05, 0}, {0.1, 0.0025}, {0.15, 0.00775},
   {0.2, 0.016025}, {0.25, 0.0276275}, {0.3, 0.0428903},
   {0.35, 0.0621793}, {0.4, 0.0858972}, {0.45, 0.114487},
   {0.5, 0.148436}, {0.55, 0.188279}, {0.6, 0.234607},
   {0.65, 0.288068}, {0.7, 0.349375}, {0.75, 0.419312},
   {0.8, 0.498743}, {0.85, 0.588618}, {0.9, 0.689979},
   {0.95, 0.803977}, {1., 0.931875}}

MatrixForm[prelimsol2]

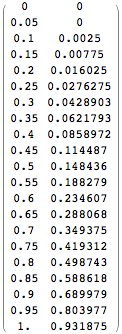
Matrix Output

The last point is now (1.00, 0.931875), which is still not as accurate as we'd like. (Remember, it's supposed to be (1.00, 1.097264).) It seems obvious that the increased number of points is responsible for the increased accuracy! To get even greater accuracy, therefore, instruct Mathematica to recalculate the solution a third time, now using 100 steps.

Let's go look at what you should have gotten...

$Compass$

If you're lost, impatient, want an overview of this laboratory assignment, or maybe even all three, you can click on the compass button on the left to go to the table of contents for this laboratory assignment.