Solving Differential Equations with Mathematica's Solver
(continued from last page...)
Your latest, hopefully successful, foray into Mathematica should have gone a little like this:
DSolve[2x E^(x^2) == Sin[y[x]]^2 Cos[y[x]] y'[x], y[x],x]

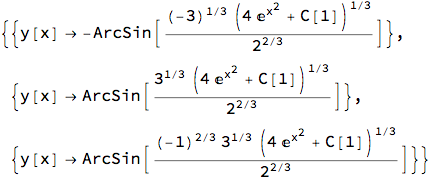
Now for a few notes about this result:
- The first and third solutions are actually complex solutions in disguise. (Notice the presence of negative numbers raised to a rational exponents!) In its usual efforts at completeness Mathematica has provided every possible answer. Where did they come from? Remember earlier when we talked about getting an explicit solution from the implicit solution we had found? One of the steps was taking the cube root of both sides! Now, contrary to what you may have learned in the past, there are always three cube roots of a number--one real, and two complex. (In general, there are always n nth roots of any number.) We would normally ignore the two complex solutions in common applications.
- The solution was put in explicit form. (It would match the one we found earlier by integrating, if we had bothered to isolate y.)
- In this type of problem Mathematica does supply the constant, though it calls it C[1] rather than just C. This is because the differential equation solver routines in Mathematica are generalized for any order of equation, and in a higher order equations, more constants would be needed, and these would be named C[2] and so on. i.e. it forms an array of constants.
We can verify the complex nature of the previous output by applying Mathematica's N[...] function to it. The function N[...] takes the decimal value of whatever is inside the brackets. We'd like to apply this function to the last output we got from Mathematica without having to retype the whole set of answers we just got. Fortunately Mathematica has a short-hand for its last output, namely %. That's right! The percent symbol means the value of the last output, so to get the decimal value of the last output we'd just type: N[%].
Go ahead and try this little command now, then come back here...
Did you see presence of 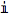 in the first and third solutions? The
in the first and third solutions? The 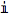 in Mathematica is equivalent to the lower-case i in most written mathematics, i.e. it stands for the square-root of negative 1—complex numbers, as we said before.
in Mathematica is equivalent to the lower-case i in most written mathematics, i.e. it stands for the square-root of negative 1—complex numbers, as we said before.
Let's go on and solve some more differential equations...







